Le théorème d’al-Kashi, ou théorème des cosinus, est un ensemble de trois relations qui sont vérifiées dans tout triangle entre les longueurs des côtés et les angles au sommet.

Ce théorème est une généralisation du théorème de Pythagore appliqué à des triangles non rectangles.

On peut d'ailleurs retrouver facilement le théorème de Pythagore. En effet, si l'angle A est droit, cos A = 0 (cf. Fonction cosinus), et la première des trois relations devient a² = b² + c² (a est la longueur de l'hypoténuse et b et c les longueurs des deux autres côtés).

Nous allons vérifier graphiquement le théorème d'al-Kashi en utilisant, comme dans notre vérification du théorème de Pythagore, des surfaces particulières construites sur le triangle initial.

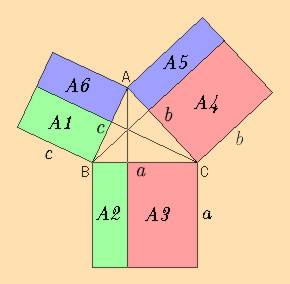Dessinez un triangle quelconque ABC ainsi que les trois carrés extérieurs qui sont portés par ses trois côtés. Tracez ensuite les trois hauteurs du triangle, que vous prolongez de telle sorte qu'elles partagent en deux rectangles le carré qu'elles rencontrent. Ces rectangles ont pour aires A1, A2, A3, A4, A5 et A6. Vérifiez, en déformant les rectangles et en déplaçant les figures résultantes, que A1 = A2, A3 = A4 et A5 = A6. Maintenant, cela devient facile : a2 = A2 + A3 = A1 + A4 = (c2 - A6) + (b2 - A5) = c2 + b2 - 2 A6. Il ne reste plus qu'à trouver l'expression de A6 pour aboutir à la première formule. Par permutation circulaire, on conclut pour les deux autres formules.