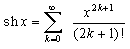Cette manipulation décrit la construction de la fonction sinus à partir du cercle trigonométrique.
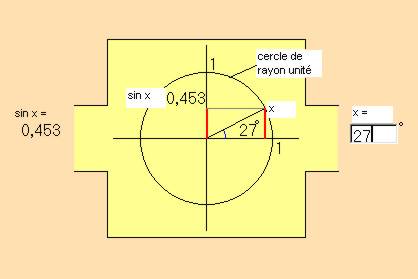
Le sinus d'un angle x est un nombre (compris entre - 1 et + 1) qui est défini comme la longueur de la projection, sur l'axe vertical du cercle trigonométrique, du rayon faisant l'angle x avec l'axe horizontal :
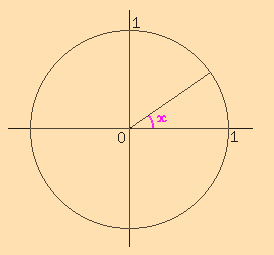
Le cercle trigonométrique est le cercle de rayon 1 centré sur l'origine du repère ; l'angle x est matérialisé par un rayon du cercle qui fait un angle x avec l'axe horizontal :
Le sinus permet, entre autres propriétés, de calculer la longueur d'un segment projeté orthogonalement, connaissant l'angle x au sommet :

BB' = AB sin x.
Une autre façon de définir le sinus est ainsi :
sinx = BB' / AB = côté opposé à l'angle x / hypoténuse du triangle, dans un triangle ABB' rectangle en B', où x est l'angle au sommet A.
Nous énoncerons quelques propriétés, facilement visualisables, de la fonction sinus.
Si x est supérieur à 0 degré et inférieur à 180 degrés, sin x est positif.
Si x est supérieur à 180 degrés et inférieur à 360 degrés, sin x est négatif.
Si vous choisissez une valeur d'angle supérieure à 360 degrés ou inférieure à - 360 degrés, la valeur du sinus obtenue est la même que celle d'un angle compris entre 0 et 360 degrés ; en effet, si n est un nombre entier, sin [x + (n 360°)] = sin x, car le rayon se retrouve au même endroit après avoir fait un nombre entier de tours dans un sens ou dans l'autre (un tour complet représente 360°) ; on dit que la fonction sinus est périodique de période 360 degrés.
Ainsi, sin 1 485° = sin [1 440° + 45°] = sin [45° + (4 ´ 360°)] = sin 45° = 0,707.
Mais la fonction sinus a d’autres symétries.
Elle est impaire : pour tout x réel, sin (- x) = - sin x ; son graphe admet le centre du cercle trigonométrique comme centre de symétrie.
Son graphe admet la droite x = p / 2 comme axe de symétrie : pour tout x réel, sin (p - x) = sin x.
Du fait de la périodicité de la fonction, ce graphe admet une infinité de centres de symétrie et d’axes de symétrie.
Les deux fonctions trigonométriques sinus et cosinus s’obtiennent aisément l’une à partir de l’autre :
par translation : sin [(p / 2) + x] = cos x ; cos [(p / 2) + x] = - sin x ;
par symétrie : sin [(p / 2) - x] = cos x ; cos [(p / 2) - x] = sin x ;
par dérivation : la dérivée de la fonction sinus est la fonction cosinus, la dérivée de la fonction cosinus est l’opposée de la fonction sinus.
Il existe par ailleurs des formules trigonométriques permettant d’exprimer les fonctions trigonométriques d’une somme (a + b) à l’aide de celles de a et de b. Ainsi :
cos (a + b) = (cos a cos b) - (sin a sin b) ;
sin (a + b) = (sin a cos b) + (cos a sin b).
La fonction sinus peut aussi être définie comme la partie imaginaire de la fonction exponentielle complexe.
Ainsi, sin x = partie imaginaire de (e ix) ou encore sin x = (e ix - e -i x) / 2i.
Cela permet d’exprimer le développement en série entière de la fonction :
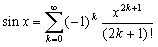
Les fonctions sinus et cosinus sont appelées fonctions circulaires. En effet, le point courant d’un cercle de rayon R centré à l’origine d’un repère orthonormé peut être paramétré par le système :
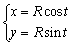
et une ellipse par :

Par opposition aux fonctions de trigonométrie circulaire, il existe des fonctions de trigonométrie hyperbolique, appelées sinus hyperbolique (notation : sh) et cosinus hyperbolique (notation : ch).
Une hyperbole peut en effet être paramétrée par le système :
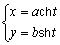
Ainsi, le sinus hyperbolique est défini par : sh x = (e x - e - x) / 2. Son développement en série entière est :