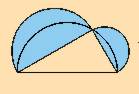
Le théorème de Pythagore établit que la somme des aires des carrés construits sur les deux petits côtés d'un triangle rectangle est égale à l'aire du carré construit sur l'hypoténuse :

Cette égalité reste vraie si, au lieu de carrés, on construit sur le triangle des cercles ayant comme diamètres les trois côtés.

Démonstration : selon le théorème de Pythagore,

AB² = AC² + BC².

Cette égalité est équivalente à :

(AB / 2)² = (AC / 2)² + (BC / 2)².

En multipliant les deux membres de l'équation par p / 2, on obtient une égalité entre l'aire du grand demi-disque et la somme des aires des deux petits demi-disques.

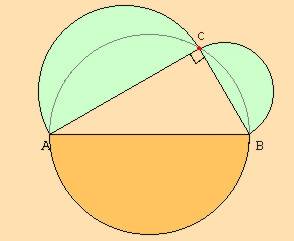
Or l'aire du grand demi-disque se décompose en une somme de trois aires : l'aire du triangle ABC et les aires des deux "segments de disque" compris entre le triangle et le demi-cercle.

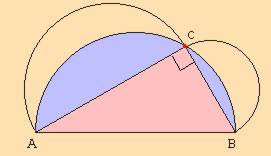
Si l'on retranche des deux membres de l'équation l'aire des deux segments de disque, on obtient, dans le premier membre, l'aire du triangle, et, dans le second, la somme des aires des deux lunules.

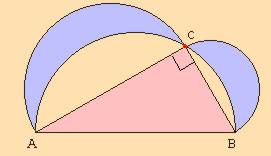
On a bien démontré l'égalité demandée.

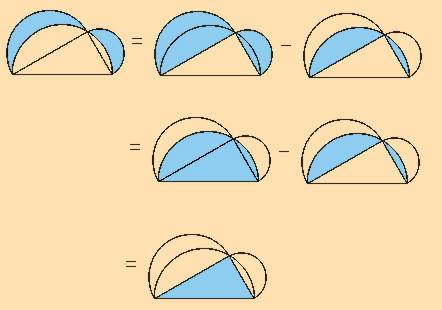
Cette démonstration peut être résumée graphiquement ainsi :